Updated 2006-10-01
| To the best of my understanding, the Optimal Jet Definition together with its fast Fortran-77 implementation Optimal Jet Finder (versions OJF_014 and later) solves the problem of jet definition. |
| It was crucial for the success of the
project that the algorithm design of the OJF library (except the last
addition described in hep-ph/0301185) was performed using the software
development platform BlackBox Component Builder (www.oberon.ch)
based on the ultra-modern, component- and object-oriented, statically
type-safe, modular, efficiently compilable programming language Component
Pascal. It is is a refinement of the revolutionary Oberon(-2) from the language design workshop of Niklaus Wirth, the celebrated author of Pascal and Modula-2. A unique combination of features makes Component Pascal an ideal platform both for the algorithm design work and the most demanding applications in computational sciences. It perfectly scales from system level programming tasks to large-scale projects while remaining a small, efficient yet superbly readable language. For more about Oberon and its potential in scientific computations see http://cern.ch/oberon.day and hep-ph/0202033. |
The public code is here (including a C++ version). It's now official:
D.Yu. Grigoriev, E. Jankowski, F.V. Tkachov:
Towards a
standard jet definition hep-ph/0301185
(Phys. Rev. Let. 91 (2003) 061801)
D.Yu. Grigoriev, E. Jankowski, F.V. Tkachov:
Optimal Jet
Finder hep-ph/0301226
(Comp. Phys. Commun. 155 (2003) 42-64)
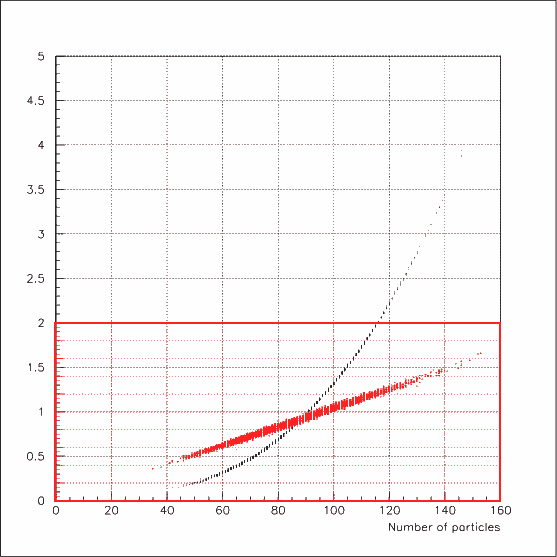
The picture below conveys an idea of how superiorly better OJF behaves ar large particle multiplicities (red) than kT/KTCLUS
(black).
The vertical axis is time in 1/100 sec per one reconstruction for kT, and for
one minimization for OJF.
The horizontal axis is the number of particles per event.

Further pictures can be found at http://www.phys.ualberta.ca/~ejankows/jets/graphs.html
A related important result is
the method of quasi-optimal observables:
F.V. Tkachov, Approaching the parameter estimation quality of maximum likelihood
via generalized moments, physics/0001019.
For references to earlier work dealing with an important special case discovered earlier by other authors, see the Jan. 2003 update of F.V. Tkachov, hep-ph/0210116.
The method of quasi-optimal observables offers a straightforward deterministic
recipe for construction of observables for theoretically optimal (i.e.
corresponding to the Fisher-Frechet-Rao-Cramer limit) estimation of a given
parameter.
A number of straightforward algorithmic implementations immediately
come to mind.
A universal algorithm based on this (something like MINUIT)
could be very useful.