Академик РАН, доктор физико-математических наук, профессор А.Н.Тавхелидзе.
Альберт Никифорович
Тавхелидзе родился 16 декабря 1930 года в г.Тбилисси, Грузинской ССР.В 1953 г. окончил Тбилисский государственный университет по специальности – теоретическая физика.
В 1956 г. окончил аспирантуру Математического института им.В.А.Стеклова АН СССР и там, под научным руководством академика Н.Боголюбова, в 1957 г. защитил кандидатскую диссертацию.
В 1956 г. начал работу в Объединённом институте ядерных исследований в Лаборатории теоретической физики (Дубна) и там в 1963 году защитил докторскую диссертацию
В 1965 году присвоено звание профессора.
В 1974 году избран действительным членом АН ГССР.
В 1990 году избран действительным членом (академиком) АН СССР (с 1991 г. РАН).
1973 – Присуждена Государственная премия СССР за цикл работ “Фоторождение пи-мезонов на нуклонах”
1988 - Присуждена Ленинскаяая премия за цикл работ “Новое квантовое число – цвет и установление динамических закономерностей в кварковой структуре элементарных частиц и атомных ядер”
1998 - Присуждена Государственная премия Российской Федерации “За создание Баксанской нейтринной обсерватории и исследования в области нейтринной физики, физики элементарных частиц и космических лучей”
2001 - Присуждена Премия Правительства Российской Федерации “За разработку, создание и ввод в научную эксплуатацию сильноточного линейного ускорителя протонов
Московской мезонной фабрики”Дисперсионные соотношения и приближённые уравнения в квантовой теории поля.
1. В локальной квантовой теории поля (КТП) установлены дисперсионные соотношения (ДС) для амплитуд фоторождения пионов на нуклонах, на основе которых, в приближении двухчастичной унитарности, для этих амплитуд получены интегральные уравнения. Ядром этих уравнений является амплитуда мезон-нуклонного рассеяния, а неоднородная часть представляет собой значение амплитуды фоторождения в однонуклонном приближении. Сравнение предсказаний этих уравнений с экспериментом даёт возможность проверить справедливость базисных требований, лежащих в основе теории.
A.Logunov, A.Tavkhelidze. JETF v32 №6 p1369-1403
2. В локальной КТП получены квазипотенциальные уравнения (КПУ) – уравнения Логунова – Тавхелидзе, которые позволяют описать систему взаимодействующих элементарных частиц (ЭЧ) на языке волновой функции, удовлетворяющей релятивистскому трёхмерному КПУ и физическим граничным условиям. КПУ весьма эффективны для вычисления высших поправок к энергии связанных состояний в квантовой электродинамике, где имеется регулярный метод построения квазипотенциала (КП). В адронной физике построение феноменологического локального КП опирается на общие принципы локальной КТП, такие как релятивистская инвариантность, унитарность, аналитичность и перекрёстная симметрия. С их помощью, в частности, исследована природа реджевского поведения амплитуды двухчастичного рассеяния, аналитическе свойства парциальных амплитуд в комплексной плоскости углового момента, дифракционная картина рассеяния на малые углы и экспоненциальное падение дифференциального сечения с ростом переданного импульса и другие. В КХД КПУ применяются для описания спектра барионов составленных из кварков и формфакторов их распада, анализа кварковой структуры адронов и ядер, изучекния процессов при больших переданных импульсах.
A.Logunov, A.Tavkhelidze Nuovo Cim.1963 v.29 №2
3. Полученные конечноэнергетические (КЭ) правила сумм для амплитуд мезон-нуклонного рассеяния, которые устаналивают интегральные соотношения между резонансной частью амплитуды рассеяния и её реджевской асимптотикой. Экспериментальная проверка КЭ правил сумм, по существу, открыла важное свойство глобальной дуальности между реджевским и резонансным поведениями. Свойства глобальной дуальности и её локальная реализация (амплитуда Венециано) сыграли ключевую роль в формулировке струнной модели адронов.
В КХД существование КЭ правил сумм (соответствующая дуальность) обеспечивается свойством асимптотической свободы. КЭ правила сумм являются непертурбативным методом, широко используемым в адронной физике КХД.
A.Logunov, L.Soloviov, A.Tavkhelidze. Phys.Lett.1967 v24B №4
N.Krasnikov, K.Chetyrkin, A.Tavkhelidze. Phys.Lett.1978 v.76B №1
Масса фермионов как результат спонтанного нарушения симметрии.
Используя открытое Н.Боголюбовым явление спонтанного нарушения симметрии, в двумерной модели Швингера – Тиринга была показана возможность возникновения массы фермионов за счёт спонтанного нарушения g
5-инвариантности теории.B.Arbuzov, R.Faustov, A.Tavkhelidze. Docl.Acad.Nauk 1961 v.139 №2
Квантовое число цвет и цветные кварки.
В 1965 г. совместно с Н.Боголюбовым и Б.Струминским, независимо от Намбу и Хана, была выдвинута гипотеза о наличии у кварков нового квантового числа впоследствии названного “цветом”. Согласно этой гипотезе каждый тип кварков с данным ароматом может находиться в трёх унитарно эквивалентных состояниях, соответствующих трём значениям цвета. Одновременно был сформулирован принцип отбора физических состояний квантовых систем, описывающих наблюдаемые мезоны и барионы, которые обеспечивают бесцветность адронных состояний. Было отмечено также, что цветные кварки могут иметь как дробные, так и целочисленные электрические заряды. В последнем случае цветовая симметрия нарушается по крайней мере в электромагнитных (ЭМ) взаимодействиях.
Квантовое число цвет лежит в основе физики элементарных частиц. Оно позволило рассмотреть цветные кварки как реальные фундаментальные составляющие вещества; гипотеза цветовых кварков, обладающих цветовым зарядом, привела в дальнейшем к созданию квантовой хромодинамики – калибровочной теории сильных взаимодействий, вызвала к жизни многочисленные варианты теории “большого объединения”.
Введение цветных ферми-кварков как физических фундаментальных частиц открыло путь к динамическому описанию адронов.
N.Bogolubov, B.Struminsky, A.Tavkhelidze. JINR Preprint D-1968, Dubna 1965
A.Tavkhelidze. High Energy Physics and Elementary Particles, Vienna 1965
Релятивистская модель адронов из квазисвободных цветных кварков.
В динамической модели квазисвободных кварков (КСК), составляющие адроны тяжёлые кварки движутся в некотором самосогласованном скалярном потенциале связь с которым приводит к компенсации их большой массы (эффект усиления магнитного момента кварка) и препятствует их вылету наружу. Модели присуще свойство аддитивности при вычислении различных физических величин, характерное для нерелятивистских моделей. Барионы и мезоны в модели КСК представляются суперпозицией всех допустимых состояний по квантовым числам SU(6) симметрии, статистики кварков в адронах и нейтральности адронов по цветному кварковому индексу.
Динамическая модель КСК позволила дать систематическое описание как статически наблюдаемых характеристик адронов (m
, gV/gA и др.), так и их формфакторов. Она позволила объяснить слабые лептонные распады псевдоскалярных p и К мезонов, а также электромагнитные распады векторных мезонов r 0, w 0 и f 0 на электронно-позитронные пары как анигиляции связанных в мезонах кварк-антикварков.Анализ данных о ширине этих распадов указывает на зависимости масштабов рассеяния (эффективных размеров) от квантовых чисел связанной системы, например,
![]()
В случае распада p
0 на два гамма-кванта, определяемого треугольной аномалией, анигиляционная модель указывает на пропорциональность ширины этого распада числу различных цветов кварков.N.Bogolubov, B.Struminsky, A.Tavkhelidze. JINR Preprint D-1968, Dubna 1965
N.Bogolubov, V.Matveev, Nguen Van Hieu, D.Stoianov B.Struminsky, A.Tavkhelidze, V.Shelest. JINR Preprint P-2141, Dubna 1965
V.Matveev, B.Struminsky, A.Tavkhelidze. JINR Preprint P-2524, Dubna 1966
A.Tavkhelidze. High Energy Physics and Elementary Particles, Vienna 1965; Proc.of the XIV Conf.on Particle Physics, Univ.of Brussels 1967
Модель КСК и масштабные законы при высоких энергиях. Правила кваркового счёта.
Основываясь на модели КСК в 1969 г. было высказано предположение, что обнаруженные в экспериментах масштабные свойства процессов взаимодействия электронов с нуклонами являются общими для всех глубоконеупругих (ГНУ) лептон-адронных процессов и могут быть выведены модельно-независимым образом на основе принципа автомодельности или принципа самоподобия. Сущность принципа самоподобия состоит в предположении, что в асимптотическом пределе высоких энергий и больших переданных импульсов формфакторы и другие размерные величины не зависят от каких-либо размерных параметров, которые могут фиксировать шкалу измерения длин и импульсов. Таким образом, формфакторы ГНУ процессов оказываются однородными функциями релятивистски-инвариантных кинематических переменных, степень однородности которых определяется анализом размерности.
Применение принципа самоподобия впервые позволило установить масштабные законы, описывающие спектр масс мюонных пар, образующихся в протонных столкновениях при высоких энергиях
p + p ® m + + m -+адроны:![]()
M – эффективная масса мюонной пары, E – энергия сталкивающихся частиц. Экспериментальные исследования этого процесса, начатые в 1970 г. группой Ледермана в Брукхевене, подтвердили данный масштабный закон. Впоследствии именно в этих процессах был обнаружен новый класс адронов – J/Y частиц.
В 1973 году, исходя из принципа самоподобия и модели КСК, была установлена общая формула определяющая характер энергетической зависимости дифференциального сечения произвольной бинарной реакции рассеяния на большие углы при высоких энергиях E = ![]() и асимптотику формфакторов при больших передачах импульса Q =
и асимптотику формфакторов при больших передачах импульса Q = ![]()
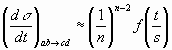
n = na + nb + nc + nd – число элементарных составляющих участвующих в реакции адронов. В случае формфакторов рассеяния безструктурного лептона на адроне, например, nb =1. Функция f(t/s), зависящая лишь от отношения больших кинематических переменных, является сама по себе размерной величиной, причём естественным масштабом эдесь является эффективный размер частиц. Таким образом, степенной асимптотический закон указывает на факторизацию эффектов больших и малых расстояний.
V.Matveev, R.Muradian, A.Tavkhelidze. JINR Preprint P2-4578, Dubna 1969;
Elementary Particles and Atomic Nuclei 1971 v2 p.6;
Lett.Nuovo Cim.1973 v.7 p.719
Масштабно-инвариантные асимптотики в локальной КТП.
Наблюдаемые в опытах масштабно-инвариантные законы в глубоконеупругих, инклюзивных и бинарных реакциях с участием адронов и лептонов, ставит вопрос в какой мере эти законы реализуются в рамках локальной КТП.
С этой целью были рассмотрены формфакторы глубоконеупругого рассеяния электронов на нуклонах
W1,2, изученные ранее Бьеркеном (1968) и для них при некоторых правдоподобных предположениях в бьеркеновской области было обосновано масштабно-инвариантное поведение т.н. бьеркеновский скейлинг.Нами прежде всего было доказано, что формфакторы
W1,2 являются причинными функциями. Далее для них используются представления Йости – Лемана – Дайсона и для весовых функций найдены достаточные условия, которые обеспечивают масштабные свойства W1,2. Для модели КСК эти условия, в частности, являются и необходимыми, которые обеспечивают бьеркеновский скейлинг в локальной КТП.N.Bogolubov, A.Tavkhelidze, V.Vladimirov. Theor.Mat.Fiz.1972 v12 №3
Несохранение фермионного и барионного чисел в калибровочных теориях и структура основного состояния.
Впервые в рамках стандартной теории электрослабых взаимодействий решена проблема нестабильности нормальной барионной материи в экстремальных условиях сверхвысоких плотностей. Показано, что ключевым свойством калибровочных взаимодействий, лежащим в основе вывода о нестабильности сверхплотной барионной материи, является сложная структура вакуума и связанное с ней сильное несохранение фермионных квантовых чисел.
Важным результатом является вывод о возможности существования в природе процессов интенсивного распада нормального вещества в контакте с каплей сверхплотной фермионной материи с мощным выделением энергии.
В рамках теории “великого объединения” предложена модель калибровочного взаимодействия со сверхслабым СР-нарушением, позволяющая описать обновременно как эффект СР-нарушения в редких К-распадах, так и возникновение барионной асимметрии.
V.Matveev, V.Rubakov, M.Shaposhnikov, A.Tavkhelidze. Usp.Phys.Nauk 1988 v156 №2
A.Ignatiev, N.Krasnikov, V.Kuzmin, A.Tavkhelidze. Phys.Lett.1978 v76B №4